The Misconception of Cosmic Space As

Appears In the Ideas of Modern Astronomy

- and as contained in the understandably limited thinking embodied

in the conceptions of the nature of parallax and redshift -

this Essay is undergoing a -revisioning,
getting even more dangerous
see new physics
~!~!~!~

      

by Joel A. Wendt

- introduction -

Before entering on to the main body of this essay, we should consider briefly the nature of thinking and of the imagination.   In this little book there are a number of different comments on thinking and on the imagination, coming from different directions, but here I want to point out some basic facts as a foundation for the coming work.

The first is that human beings think, and that there is no science without the activity of human thinking.   Thinking determines which questions the scientist asks, what experiments he conducts, and then ultimately how the data provided by the experiments is interpreted - that is what does this scientific activity mean.  For this essay we are confronted with the scientific meaning created by human thinking in relationship to some considerable portions of the data accumulated by scientific work centered on questions concerning the stellar world.  We are asking here in this essay whether what science thinks today of the meaning and significance of the stars is what we ought to continue to think, in the future, or even today to assume is still a reasonable understanding.

"Christ Blesses the Gray"s, by themikehoffman

As scientists all possibilities need to be on the table ... anything less is a fraud ... still, if you are afraid of the dark, or of the mysterious, then maybe this place is not for you, ... but if you want to adventure, and still be scientific: The Fermi Paradox Resolved discusses generalities, here we get to nuts and bolts.  Just keep in mind there have been astronomers since there where eyes to see stars ...

                                                                     

As part of the process of examining the underlying questions, we will be using a particular capacity of the mind, which might be called the imagination, or picture-forming  capacity.   We make all manner of mental pictures in the normal course of ordinary thinking, and in scientific thinking we carry out this activity in quite specific directions.  Certain astronomical ideas, for example the idea of parallax, are specifically grounded in the picture-thinking connected to Euclidean geometry.   While we sometimes use a pencil and paper to work out the details of this geometric picture thinking, the fact that should not be ignored (but often is) is that it is the mind of the human being that contributes the fundamental activity from which our modern astronomical conceptions arise.  In fact, our interpretation of the meaning of astronomical data is entirely a result of mental processes, a number of which are expressly born in the imagination.

Yes, we carefully observe the stellar world with all kinds of remarkable instruments.   We also use a great deal of mathematics in how this material is interpreted, but we must never, in the process of unfolding this scientific investigation of the world of the stars, forget the centrality of thinking and of the imagination to the whole process.   If we take thinking and the imagination away, there is no science of astronomy.   Why this is so important will hopefully become more clear as this essay unfolds.

- main body -

                                                                                                                                           

*"Our Father in the skies..."  are the first words of the Lord's Prayer, as translated by Andy Gaus in his book The Unvarnished Gospels.  I start here to point out the fact that the people living in ancient Palestine, at the time of the Incarnation of Christ, had a different kind of consciousness than we do today.   When they looked at the heavens, they understood (and were taught by their wise elders) that the sky was the abode of the Divine Mystery.  In fact, they understood the whole of Creation to be en-souled with Being and Consciousness.   Since that time a different conception of the heavens and of the earth has come into existence for large portions of humanity.  How did that original conception change and what can we learn by observing carefully the nature of that change? 

Everyone understands that if we make even the slightest error in the aim of the bow and arrow, by the time the arrow reaches the end of its journey, it doesn't take much of an original error to cause the arrow to have completely missed the target.  Human beings are flawed, and science is the activity of human beings.  In the following essay I am going to concern myself with clearly amateur* researches and thinking into the problems of parallax and red shift, as these ideas are used to create for us a conception of the world of the Stars.

Johannes Kepler thought we were in danger of throwing out the baby with the bathwater,
 in our wholesale rejection of the ancient understanding/knowledge of the starry world.

                                              

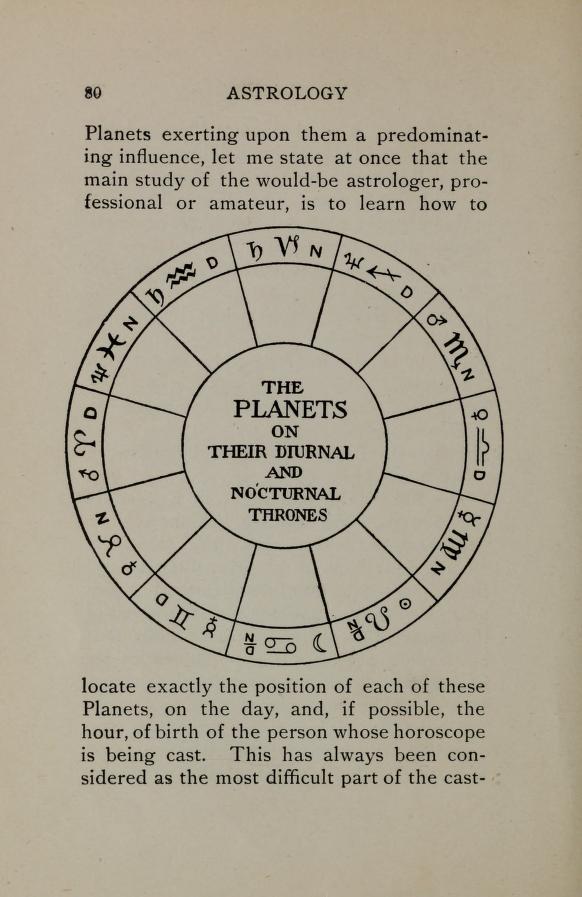
                                                                                                                                   the best of ancient lore on the stellar world is here:
                                                                                                                      Practical Astrology by, Comte C. de Saint-Germain
                                                                              no other book on the ancient stellar wisdom combines into a single system:
                                                             astrology, tarot, and numerology - want to know why?  Study that book...

                                                      

*[While I am not a member of the priesthood of the religion of Natural Science, I do know how to observe carefully and how to think objectively, so just because astronomy isn't my profession, the reader should not automatically anticipate they will be misled.  The reader should, however,  themselves test the themes outlined below in their own careful picture-thinking.  The tendency of scientific thinking has been toward too much  analysis, and not enough synthesis, while the return of a focus on the imagination will help us move forward in the future toward a needed  balance between these two basic gestures in thinking.]

The fundamental question is this: the current generally understood idea of cosmic space is that it is essentially a three dimensional endlessness - a very big box, which while it must have some unusual properties as a container, it is nevertheless organized such that everywhere inside it one can expect that the same rules of physics we observe in the laboratory on the Earth, will be true all that way out there...one upon a time in a galaxy far far away.   Is this conception of endless three-dimensional space true?

Let us consider a rather simple geometric thought experiment, which everyone (trained mathematician or otherwise) can do.

                              learn about casting/generating this figure: 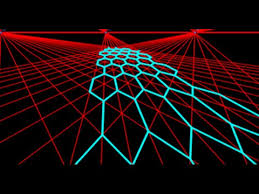   AKA: hexagon net in stepwise measure ... <here>

Make a picture of a small perfect sphere in your mind.  It has a center and a periphery.     That is the nature of the bubble in physical space, where individualizing consciousness exists.  A machine can't write this stuff, given that only a human being reads-into words what we do ... also individually.
We are point centers of consciousness, wandering troubling seas ... We are love&magic, ... or not  <shrug> ... Sense8 sentience - all minds connected - best scale is local, and to music - dancing ... 

 One can use the terms radius, circumference and diameter with respect to this sphere, but they really don't have any exact meaning unless we define one of these characteristics by giving it first an exact measure.  For example, if we said the radius of our mental sphere was one meter, well understood rules of the geometry of a perfect sphere would give us diameter and circumference (as well as other related characteristics, such as the degree of arc of the curvature of the surface, the area of the surface, etc.). 

The inner geometry of center and periphery - my ~!~ experience.  Every object, inert or otherwise, has existence certainly.  Why deny/pretend that all the ITS&THINGS also  have consciousness and will?  The "smartphone" robs our ability to remember, saving all kinds of data reducible to code.  Alladin's Lamp, with a dash of Dick Tracy's wristwatch radio - dangerous waters as we borg ourselves and pretend that the stuff ... well, a tool is only as good as the tool user.  The best tools are hand crafted from scratch, and given ceremonial rites - everything is sacred - even hell.  >"Shamans" 0ogle images here>

every object, every surface, every place where we see, light-is-with-darkness, or there is no color ...

Now keep in mind that we don't have to conceive of this sphere in terms of measure.  It can just exist in our mind as a measureless perfect geometric form. 

Next, we imagine the radius line, from the center of the sphere to the periphery, increasing.   We again don't have to measure it, we just make the picture in our thinking of this imaginary sphere as something that is slowly growing through an elongating radius line.   The radius line grows.  As that line grows all the other characteristics of the sphere grow as well.

We could also mentally cause the same effect by changing any other  properties.  For example, if we cause with our picture-thinking the area of the surface to increase, we change at the same time all the other relationships.

Now lets return to the increasing of the radius line.   In your imagination now picture that intersection between the radius line and the periphery of the sphere.  At this intersection there is a degree of curvature of the arc of the sphere.   We can notice as we do this thought experiment that as the radius line grows, the tightness of the curvature of the surface lessens.

To help this, lets imagine the radius line decreasing.   We shrink it, and as we do this the curvature of the periphery of the sphere gets tighter and tighter, until we make the radius line zero.   When we make the radius line zero we have lost the sphere, and it has disappeared into a dimensionless point.

Yet, since we are working without any need for measure, a zero radius sphere is simply a point.  Once we give measure of any amount to the radius line of a zero radius line sphere (a point), the sphere returns.   A radius line of a nanometer takes a point and makes it a sphere.

Seeing this clearly with our geometrical imagination (which is quite exact and precise, by the way), we now do the opposite and complete the earlier exercise by increasing the radius line to infinite length.  Instead of a radius line of zero, it is now infinite.  What then happens to the curvature of the sphere when the radius becomes infinitely elongated? [For a delicious discussion of "infinity" see David Foster Wallace's: Everything and More: A Compact History of Infinity.]

Well, if we carefully follow out our precise and exact geometrical imagination, we will be able to observe this process unfold.  As the radius line increases in length the original tightness of the curvature of the surface of the sphere lessens, until at the moment the radius line is infinite there will be no curvature at all.  The sphere has disappeared, and undergone a metamorphosis into a plane.   If we think carefully about what we have learned here, we will see then that any sphere of any measure of radius line is always an intermediate geometric form arising in between a dimensionless point and a plane at infinity.

This fact is already well known in the profound mathematical science of projective geometry, and we have now ourselves discovered what is called there: the Plane at Infinity.  The sphere then is geometrically in between the infinitely large and the infinitesimally small, or in between the plane at infinity and a geometric point (which has no measure at all, unless we put it into relationship with something else).  A point by itself is just that - nothing else.  It occupies no space at all.

Well then, what is the point of this exercise?

There are several.  First it is crucial to realize that we can think geometrically without using any measure at all.  If one is lucky enough to come upon a copy of Olive Whicher's Projective Geometry: creative polarities in space and time*, one has the possibility to study this wonderful geometry using only a pencil, a straight edge and some paper (large sheets are easier for some constructions).   Measure has been done away with, and the creators (or discoverers) of this mathematics describe it is all geometry - meaning by this that every single other geometry is a special case of projective geometry.  Also George Adam's Physical and Ethereal Spaces.

*[check Waldorf Schools or other Rudolf Steiner institutions for copies of this book.   It is often tragically out of print.]

The difficulty for Natural Scientists has been how to apply this beautifully symmetric, measure free geometry, to the natural world.  Science is rooted in measure, and while the ideas of this geometry are recognized as significant, what could they mean in a world that is already hopelessly entangled in a science which has to use measure for everything?

With this riddle in the background, let us now examine the history of ideas by which the old view of the heavens as an abode of the Divine Mystery came to be supplanted by a view in which space is conceived as a near endless three dimensional container, punctuated with mass caused curvatures (the space-time gravity ideas following after Einstein, using the Reinmann geometry - again a special case of the more general projective geometry).

Giordano Bruno, who was burned at the stake as a heretic in 1600, is credited with having first suggested the idea that a star might be like the sun.  Would that our histories were more accurate, because what we think of as the sun today, and how he thought about such matters (he was, among other disciplines, a deeply thoughtful meta-physician*) is not quite grasped by believing his idea, that a star and our sun were relatives, in fact mirrors in anyway our modern conceptions.  For Bruno, the idea that a star and our sun were related, was a completely different idea than we hold today. The details of that, however, is a whole other matter.

*[Meta-physics, contrary to modern views that it is not a science at all, was really always seen as a product of a synthesis of ones total understanding.  Modern physics comes from taking things apart, from analysis.   Meta-physics always had the task of make the parts of all human knowledge into a single whole.  For a good example of modern thinking that is "wholistic", as regards astrophysics, read Georg Blattmann's The Sun: the ancient mysteries and the new physics.]

Bruno did agree to a degree with Copernicus, and so in those years the ideas being produced by natural philosophers (the grandfathers of natural science) came to be at odds with the dogmas of the Roman Catholic Church.  While the previous age of careful thinkers (the Scholastics), would have understood (keeping to Aristotle) that there was a difference between quantities and qualities, the scientific impulse coming to the fore in those years more and more felt it could only deal with that which could be counted or measured - that is quantities.   The various categorical qualities of Aristotelian meta-physics more and more dropped away from consideration (although this was a long term process and many thinkers (Kepler and Faraday, for example) thought this was an error of thought to do so.

In any event, pure astronomy slowly freed itself from the meta-physics connected to astrology and related disciplines, by a process in which the qualitative problems were left aside and everything was more and more rooted in only what could be counted (and measured).  Kepler, it has been forgotten, was an astrologer as well as the discoverer of the three fundamental laws of planetary motion*.  Not only that, but Newton was an alchemist.  The tendency has been to frame the history of these thinkers as if they thought as we do today, when anyone who actually reads what they wrote discovers they did not. (For a comprehensive examination of this overlooked history of science, read Ernst Lehrs' Man or Matter: Introduction to a Spiritual Understanding of Nature on the Basis of Goethe's Method of Training Observation and Thought.  Also read the physicist  Arthur Zajonc's Catching the Light: the entwined history of Light and Mind.

*[Kepler believed, for example, that his formula and ideas regarding the Third Law of Planetary Motion was a rediscovery of the ancient's idea of the Harmony of the Spheres]

As this process matures, it reaches a kind of high point in the 19th Century, and two important ideas are given birth out of the context of this leaving aside of the problem of qualities, and resting all theories of the starry world only on what can be counted and measured.  These ideas are  parallax and redshift.  Such concepts don't emerge on their own, so we have to work carefully with them, still keeping in mind how dependent they are upon measure alone.

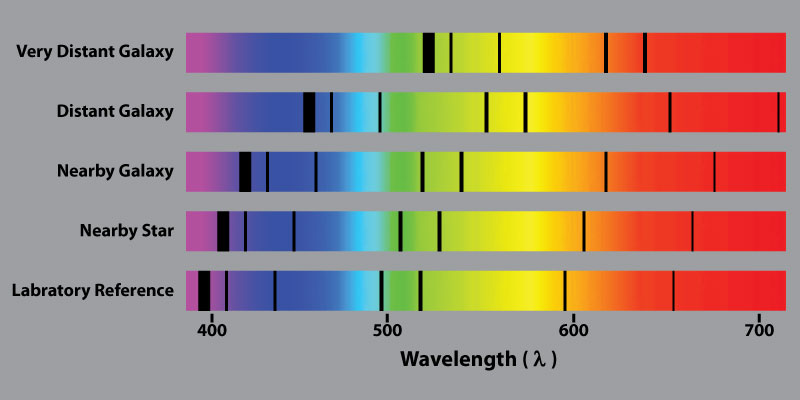
The idea of redshift doesn't come by itself, for example, for it is really based upon spectroscopy.  This science is itself not based initially on stellar observation, but on work in the laboratory where various fundamental elements are combusted (burned) in such a way that they produce "light".  This "light" is measured according to the quantitative ideas of Newtonian Optics, and so we get the "spectral" lines for such basic elements as hydrogen.

As a result stellar light phenomena, including light phenomena from our sun, are used in such a way that it is assumed that this light from the stars, and our sun, is produced in those places by a burning process similar in kind (but not degree) to what was done in the laboratory.  If the light from a star, or our sun, has a certain mathematically accurate vibration (frequency), that is like or essentially similar to the hydrogen line obtained in the laboratory, this light frequency is then seen as showing us that in that star, or our sun, hydrogen is being burned up, which combustion process gives off that particular light frequency.

This is so important a fact (actually assumed to be universal) that in the movie Contact, the frequency used to send the message to Earth from the fictional stellar civilization is the hydrogen light frequency times pi.  That is, it is a material constant multiplied by a geometric constant.

All the same, there was a problem with the hydrogen light frequency, for example, from the stars.   The observed light frequency in the normal range for hydrogen (assumed to be an exact universal constant) isn't actually quite so exact to observation.  Various stars' hydrogen lines are discovered to be a bit off center, so to speak, such that they can be described (in the assumptions of physical astronomy) to be either red shifted or blue shifted.  The greatest number of stellar objects are red shifted (only a very very few are blue shifted).

Following Newton, color is a spectrum of light frequencies, with a red end point, where beyond which it becomes invisible to the eye, or a blue end point (actually violet, but convention names that end of the spectrum the blue end) where beyond this end it also becomes invisible to the eye.  We see with our eyes a normal color Newtonian spectrum (so it is assumed) and at the edges of this visible spectrum the light is no longer visible, although it still can be observed and measured with instruments (the red end becomes infrared or heat, and the blue end becomes ultraviolet, leading then to such as x-rays).  The wavelength of the frequency at the red end is longer and longer (elongation), and the wavelength of the frequency at the blue end is shorter and shorter (compaction).

These questions arise: what does it mean that light from the stars is not exactly showing us the precise hydrogen line we came to know in the laboratory, and what do we make of the fact that this shift toward the red (the dominant types of shift) itself varies?   Some stellar objects show small redshift and other's quite large redshift.

The original dominating idea for the meaning of the phenomena of the redshift (elongation) of such as the hydrogen line frequency was arrived at by creating an analogy between light waves and sound waves, in 1842.  We all know (or experience at least) the so-called Doppler effect - the shift in sound of a train horn as it comes toward us or away from us.  This movement toward or away produces a change in the pitch (auditory frequency), even though we know that the actual pitch the horn is making never changes.  The change in pitch is heard because of the movement of the source of the sound (which compacts or elongates the frequency, as perceived by the ear, which is relatively stationary).

By analogy then, redshift was thought to give evidence of the movement of the object away from the observer on the Earth.  Whatever was going on, most of the stellar objects had this redshift phenomena (in varying degrees) and from this analogy was born the idea that the Universe is expanding (which then later is supposed to logically give us the Big Bang - an explosion which creates an expanding Universe).   I point out this last to urge the reader to notice how interwoven are all the ideas we have today about the physical universe, such that if, for example, redshift doesn't really mean what we think it means, then this idea of the expansion of the Universe loses one of its main supports. (See link at end of essay for current thinking on this problem in conventional astronomy.)

The first problem to arise after the more or less universal acceptance of this theory, was the recognition that while light was superficially a wave  phenomena (a movement propagating in a medium), similar to sound, the analogy didn't really hold, so a lot of thought went into how to revisit the redshift phenomena and appreciate it better.   Unfortunately, while many scientists feel certain older kinds of ideas ought to get dropped away from any current point of view, some ideas seem quite unwilling to be abandoned, so the Doppler analogy remains, even though contemporary physics sometimes sees light as both particle and wave simultaneously (depending on what questions you ask, and which experiments you do).

One of the newer theories as regards redshift (moving away from the Doppler analogy) is that it is partially a consequence of the temperature in the star.  Another sees some redshift phenomena as reflecting the influence of gravity wells.

I point this out only to suggest that theories themselves are in constant motion (a kind of social Brownian-motion among different minds).  I am not so much interested in the current theory here, because it is my view that the resolution to the fundamental question lies in a quite different direction.

Let us now leave redshift behind, and go on to the idea parallax, which arose a few years before redshift historically (1838, so it says on-line).

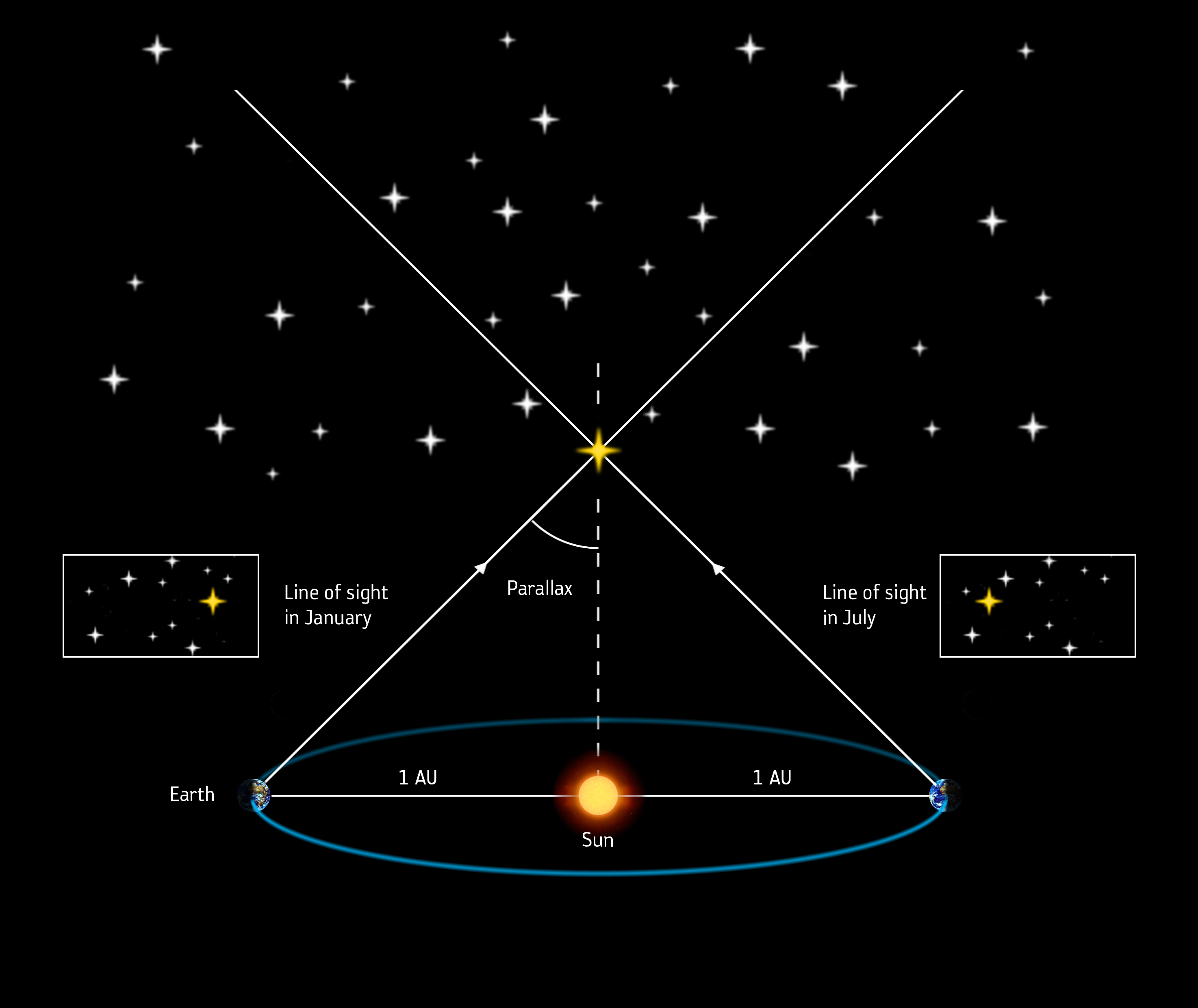
The basic idea of parallax is that it enables us to measure (remember what was said above about measure) how far a star (or other stellar phenomena) is from the Earth.  Basically this is done by coming up with an observational angle, that can be measured on the Earth, and is made possible in large part by the orbit of the Earth around the sun.  Since I can't put in a drawing here (the reader can go on-line if they desire) I'll try to do this with words.

Place on the grass of a football field, in your imagination, two poles.  One pole is at the center of the goal line, and the next at the center of the 10 yard line nearest that goal line.   Now go down to the goal line at the other end of the field, and set up a transit (a device for taking the measure of an  angle of changes in a sight line).   Move the transit from one side of the field to the other, stopping every yard, and make observations of the angle of observation between the two poles obtained by viewing them from the moving transit.

As we do this the angle we are measuring changes.  This angle is widest at one side of the field, and then contracts, until we are right opposite the two poles (at which occurrence the near pole occults the other, or stands in front of it), and then the angle expands again as we move toward the opposite side of the field.

Now imagine such an activity taking place with respect to the light phenomena of stellar objects.  The transit is actually the earth, which moves constantly, changing the observational "angle" with respect to distant objects.  As this earth-transit moves, some of the distant objects seem to occult each other, as if one was in front, and the other behind.

However, since these objects are so far away (apparently), the angles that are measured are very very very small (small fractions of seconds of degree of arc).  One writer suggested that if you took a quarter, and looked at it from a distance of three miles, measuring the angle between a transit observation of one side of the quarter, and then the other side - this picture suggests how small an angle is actually being measured by this method (parallax) with regard to the nearest star to the earth (for stars believed to be further away, the "angle" is progressively smaller).

Using this data (the angle measurements coupled with our knowledge of the diameter of the Earth's orbit) we can use the basic rules of Euclidean geometry to determine the length of the sides of the resultant triangle.  This information (with a couple of other geometric ideas rooted in measure) then gives what we think to be the distance of the stellar object from the Earth.

Now since redshift is believed to tell us that most stellar objects are moving away from us, these distances change over time, which then appears to give us a kind of confirmation of the parallax.  The problem is that some of these observations came in conflict (an inconsistency between redshift and parallax).   One of the most obvious of these was discovered by the astronomer Hal Arp, who as a result for a time found himself to be seen as a heretic by his fellows, and was temporarily shunned (couldn't get telescope time to continue his research (see his book,  Quasars, Redshifts, and Controversies).

Basically what he observed (using conventional astronomical ideas and methods), was that Quasars (quasi-stellar objects), while they had a very high redshift (suggesting they were traveling very fast away from us, and since they were thought to have been doing this for some time - no changes in rate of velocity and/or acceleration were assumed, they were also thought to be quite far away, while the parallax measurement seemed to imply they were much nearer.  Quasars seemed to occult (get in front of) much slower (less redshifted) stellar objects).  The two phenomena could not be reconciled.  Were Quasars near or far?

I'll not go into what were the conventional adjustments made (its all very complicated, and unnecessarily so in my view) in order to preserve the basic set of ideas of modern astronomy, but we can (with justification) simply step past these ideas.  Why?

Because fundamentally the problem is due to the fact that phenomena of redshift and parallax is organized in accord with Euclidean geometry and the need in science to measure.   In effect, at every point in the development of these ideas (though scientific thinking and imagination), we exported to Cosmic Space those conceptions that were true here in the center (the Earth), and further, we assumed* that these conditions were an invariable constant.

*[There is no empirical evidence for this whatsoever - it is 95% theoretical.]

For example, the distance we measure using the idea of parallax can't actually be tested empirically.  In essence, we export from our Earth reality the concept of Euclidean three-dimensional space to the apparently farthest reaches of the starry world, but at the same time have no way of testing the set of assumptions behind the activity of exportation of such an idea.  We can't go off to the side of the container in which all stars are held, and measure from another quarter whether in fact the distance the parallax formulation gives us is correct.

For another example, we find the hydrogen frequency line by a laboratory experiment here on the surface of the Earth, and then assume that nothing of physics changes at cosmic distances, and that the universe will obey the same laws way out there that it obeys here.  Under the influence of these assumptions we export our earthly picture to cosmic spaces, something that really isn't justified if science wishes to remain properly empirical.

All our observations are made on the Earth or from near-earth space.  It is really only in our mind that we go outward toward cosmic space.   If that is the case, then we must be very very careful in how we let one thought grow from the other.   Clearly if there is an error in thought (remember our arrow to the target analogy at the beginning of this essay), then the further out in space our imagination, of the picture of the meaning of the data we collect here goes, the more a small error in our thought will produce a quite large miss in our understanding of the truth.

While there were many small mistakes made (such as the assumptions observed regarding the hydrogen line), there is one single idea that saves the situation as it were.  We set aside Euclidean geometry and substitute for it Projective Geometry - the fundamental geometry of which all other geometries (including Euclidean) are a special case.  Let us next then try to apply this geometry to the image creation aspect of our thinking, because after all it is the image we are making of cosmic space that is important.  It is the mind that travels to cosmic space, riding the ideas we have created from the data only empirically observed here.  We, who live today, have traveled far down the historical path of one kind of mind-created image, and now it is time to perhaps deconstruct it and create something new.

Lets recall the older (or current) image first, namely of a three dimensional emptiness, filled with stars which are like our sun, some surrounded by  planets like our planet.  It is a powerful image.  Science fiction, books and films, tell all kinds of tales.  If one were to suggest that this might not be correct, most people would think you were crazy.

Return now to our earlier work in which we expanded the radius line of the sphere to infinity and observed how the sphere became a plane at infinity (or the reverse, where if we contract the radius line the sphere disappears into a dimensionless point).  Also keep in mind that the geometric form never changes its basic nature - it just transforms at the different extremes (the infinitely large and the infinitesimally small radius aspect).

A lot of people should have some trouble here, because they conceive of infinity as something much larger than say the multiple light years of measure we have applied to the distance between the Earth and the stellar objects.  In this regard, lets look at some apparent facts so far developed under the old methodology.

For example, the so-called nearest star, Proxima Centuri is thought to be 4.2 light years away (its degree of arc in parallax is .77233 seconds of arc - which is by the way the largest degree of arc using parallax measures, for every more distant object will have a smaller degree of arc).  4.2 light years (this next is an amateur calculation) is 24 billion miles (that's 24,000,000,000, or 24 thousand million).   The farthest distance objects are high multiples of that.  We'll return to this a bit later.

Remember, we have exported an idea to cosmic space which we can't empirically test.  Science, tied to the idea of counting and measure, has exported to cosmic space a measure (huge light year distances), which idea can't be checked by any other means.  As a result, we are quite right to challenge this exportation of measure to test whether it is a thought that is properly rigorous.  Since we cannot empirically test the assumed measure, we are left with the quite definite necessity to even more carefully and rigorously subject that idea to the tests of logic.

Here is a very important question.  If at the center of our infinitely small sphere, the point, there is no actual space, once we have created any measure of radius distance (a nanometer, for example), we now have three dimensional space, then what happens at the infinite radius, when the sphere disappears and becomes the plane at infinity?  Is this transition as apparently sudden as the one from the point to the very very small sphere?  [Again, for a delicious discussion of "infinity" see David Foster Wallace's: Everything and More: A Compact History of Infinity.]

If we actually think very carefully about this we will notice (using our geometric imagination) that even the transition to the very very small is not sudden.  There is a lot of work on theses themes in mathematics, and you can Google it by starting with Zeno's paradoxes.   In any event, at the infinitesimally  small end of the transition, from the sphere to the point, the process itself is likewise smaller and smaller in nature, while the transition from the very large sphere to the plane at infinity must, by virtue of laws of symmetry common to projective geometry, be larger and larger in nature.  Keep in mind we are thinking here of the transformational process, from one geometric state or form to another state or form.

The plane at infinity doesn't appear suddenly out of nowhere, but as we approach it the nature of three-dimensional space is slowly undergoing a metamorphosis.   Three-dimensional space is becoming plane-like in its fundamental nature, but not all of a sudden.   Space itself is changing, and the rules of physics applicable to a purely three-dimensional sphere (Earth conditions) will no longer, at these extremely large distances, apply.

What are huge light year imagined measures then (such as the 78 billion light years assumed for diameter the visible universe - there being thought to exist a greater universe we cannot yet see even with our instruments)?  They are simply a fantasy or myth, born in the assumptions of the scientific imagination.  Since we cannot conceive of anything as knowable scientifically, without measure and counting, we presently are unable to conceive of the universe without measure either.  Again, an assumption that causes the arrow to miss the mark.  The question right here then is whether the current limits of our imagination and thinking reflect the actual limits of reality.  Confined for a time in the limited box of Euclidean Geometry, we stand on the cusp of transcending those limits by applying the more universal Projective Geometry.

This should not surprise anyone, for we already know that in particle physics, where the transition of matter endowed space becomes infinitesimally small (remember the sphere collapsing into the point - which has led us into all the paradoxes of quantum physics) the conditions there are suggestive of all kinds of alterations of the rules observed at a more (relatively) macro scale of matter.  At very small dimensions, the rules of physics change, so why would we be surprised that at very large dimensions, the rules of physics will also change.

In fact, in the wonderful movie Mindwalk, the character of the physicist describes matter as a huge emptiness, punctuated with geometric points, where fields of force intersect.  In effect, there is nothing there at all in terms of substance (or what we call matter) but this organism of intersections of fields of force in various kinds of pure geometric points (no space).  No space at the infinite periphery, and no space in the infinitesimal point.  In between, the perfect geometric sphere mediates between the greatest and the smallest.  "Think on it: how the point becomes a sphere and yet remains itself.  Hast thou understood how the infinite sphere may be only a point, and then come again, for then the Infinite will shine forth for thee in the finite."  Rudolf Steiner.

Now if this is true, then as macro cosmic space becomes more plane-like and less like the normal physical conditions of the Earth, we ought to be able to observe phenomena (just as we do in the very smallest dimensions revealed by quantum experiments) that reveal to us that this condition of space itself has altered.  Space, being no longer three dimensional at the plane at infinity, must become something else.

Before we believe this is a poor idea, recall that already we have been taught about the so-called gravity wells (especially near such objects as our Sun).  Many of us have seen images, either on TV or in a page in a magazine, which suggests that near a massive object, space itself is distorted.  Light, we are told, traveling near this imagined state of a gravity well, can't travel in a straight line.  This is thought to have been proved by Einstein's predictions regarding light from Mercury as it passes toward us from the other side of the sun (when Mercury's orbit causes it to hide (be occulted) behind the Sun.  Using the Reinmann geometry (a special case of projective geometry) Einstein was able to calculate exactly the amount of the bending of light by the gravity well our our Sun.

Since we already know how to imagine a distorted near space around a massive object like our Sun (recall that Bruno thought our Sun and stars were of a similar nature) it is not too great a leap to imagine a fully  transformed space at the transition from the very large sphere to the Plane  at Infinity.  In a sense, the image of gravity wells is already a transformation of our ideas of space itself, although not going so far as to free itself fully of the need to measure.  What I am suggesting is that we take our spacial imagination faculty all the way, and also bring projective geometry itself all the way into play as descriptive of the natural world.

Keep in mind that in current theoretical astronomy, scientists are unable to explain stellar motion without adding to their assumptsions about the total visible mass of stellar objects, 9 times more mass in the form of the so-called Dark Matter.  Estimates of the total mass of visible objects can't explain apparrent stellar motion (using conventional ideas), so, in order to save the theory, invisible mass - Dark Matter - has been invented.

But this invention is unnecessary if we use projective instead of Euclidian geometry.  Which is of course exactly what our observations of light, and other phenomena of the stellar world, can tells us if we let them.  Once we overcome the one-sided Euclidean geometry previously applied in parallax, and substitute Projective Geometry principles, then all the anomalous problems of redshift and other mass-centered problems are resolved.
 

The reason the hydrogen line of stellar objects is different is because it (the light) originates in a kind of space which itself is different).  A star isn't a sun (unless we change our ideas of our near sun-space - going back to Bruno, which is entirely justified but a whole other problem).  Those stellar objects with large redshift characteristics (such as Quasars) are deeper (a presently necessary poor choice of words, for it implies a continuation of three dimensions) within the transformed plane-like space.  In fact, if we make a picture only of the redshift (disregarding Euclidean parallax) phenomena by itself (and related other astronomical facts of stellar radiation and mass phenomena), a new kind of picture emerges.

Think for a moment on all the pictures we have been graced with of the starry world from the Hubble telescope.   Everyone has seen these.  Rich colors, but not empirical [See "How Do Space Pictures Get So Pretty - Photoshop of course"].  Marvelous shapes and forms.  Just looking at the redshift characteristics we can make a picture of an object that is remarkably active.  It is not static or at rest in relationship to the Earth, but dynamic.  Its relationship to other stellar objects is more fixed (perhaps musically harmonious, because there is a dance of such objects - including our solar system - all based on the projected geometric form of the vortex*), but the light phenomena, which our instruments observe, suggests (since we observe this variation of redshifts, x-ray stars etc) that stellar objects have dynamic properties.  The various kinds of radiation, pouring toward the earth from the cosmic periphery, are not constant, but rather always changing and dynamic.

*[A vortex is, in terms of projective geometry, a dynamic form.  That is, it is, in its actual nature, in movement.  A tornado funnel cloud is a vortex, and we see a vortex every time we flush a toilet.  A vortex is also a relative of the cone of light, which is how we think of what light does when it enters the eye through the lens.  These cones of light are well described in all their geometic properties by the rules of projective geometry; and, a vortex is simply a dynamic (moving) cone-like form in nature.]  [See the amazing visual art of DjSadhu]

Many stellar objects are extremely dramatic (x-ray and neutron stars, for example).  Keep in mind that these pictures are created by a thinking which has removed all qualities, remaining only in quantities.  To better appreciate this lets make a little analogy.

Consider a flower garden in full late summer bloom.  Vivid colors, lots of insect life and birds dancing and playing.  For some almost violent growth (how fast does a sun flower grow, on its way to a height of 12 to 14 feet in three months time).  Of course, to the gardener it makes no sense to disregard the way such a garden makes us feel (its qualities), but if astronomical thinking were applied to a flower garden, all that would disappear.  We'd end up with a bunch of numbers (how many, of which kinds, what frequency of light were the colors, what was the speed of growth etc. etc. etc.).  Our actual experience of the garden is washed away by the process of limiting our thinking only to the quantitative.

Now think (if you can remember) of a time when you were deep in Nature, away from city lights, and lay on your back in a meadow looking up at midnight at the night sky.   Thousands upon thousands of stars, and your mind naturally saw everywhere patterns.   Moreover, we feel awe.  The starry night touches something deep inside us, that can only respond with marvel and wonder.  We forget this living in our cities, and we have also forgotten (and losing) even the ability to have such a view because the atmosphere itself is becoming so polluted that less and less of the stellar light passes through it to our eye.  [For a more careful discussion of the nature of consciousness as regards qualities and quantities, go here: "I am not my brain; the map is not the territory".]

This is what we observe - what we experience.  What we think - what is our mental image or picture - having been formed by modern astronomical ideas, is that this endless emptiness is filled with objects like our own planet and solar system.  But now we are discovering in this essay the possibility that deep space is not three dimensional at all.  Cosmic space is a peripheral plane of light, alive with dynamic processes creating what?  What is this new kind of space - the plane at infinity - from which stellar light pours down upon the Earth, and then becomes captured by our photographic processes?  The light from the stellar world is dynamic, and when we make an image (Hubble stares at certain regions of space for 10 or 11 days at a time), we have eliminated that dynamism, and made the picture static or fixed.

Lets take a small side trip here, to consider light itself.  The book mentioned above, Catching the Light: the entwined history of light and mind, goes into remarkable detail and history.  Keeping our projective geometry idea in mind, we might then make a relationship between the sphere that has collapsed into a point, and what is now called light quanta or photons.  As mentioned above, these quanta exhibit all kinds of properties that normally spacial (in a three dimensional sense) objects do not.

For example, the world we see of trees and clouds does not reveal the micro world of light quanta and the other many strange particles known to modern high energy physics.  The scientist doesn't see much of this either, except with his instruments and the image making powers of his mind.

We could say (from our more naive point of view - which has a special validity) that it is as if light quanta have stepped outside of time and space (this is one way of viewing what the experiments with light show to us today through quantum physics).  To help here, let me add another idea from projective geometry.

We know in Euclidean geometry this general rule: parallel lines never meet.  In projective geometry (of which, remember, Euclidean geometry is a special case) parallel lines meet at infinity.  To appreciate this better we need to practice another imagination, for we can with our picture thinking follow quite easily in thought the wonderful paradox expressed here.

Picture two parallel lines (I can do this here):

_______________.________________

________________________________

Now imagine the top line, in the center of which is a point, rotating around that point.  Picture, for example, the top line crossing the bottom line at about a 45 degree angle toward the left side of the page.  As we rotate this line further to the left, the angle of crossing gets smaller and smaller, until at infinity it no longer crosses the line.  Yet, if we keep rotating the line in the same direction of rotation, as soon as it goes the smallest possible distance further, the top line starts to cross the bottom line at the farthest distance to the right.

When we couple this idea with our appreciation of the plane at infinity, we can with our geometric imagination feel (picturing it is hard, but logically we can feel this is right - and all these ideas have been proved by those working with the rules of projective geometry using algebraic-like formulas and calculations) that these two lines, which could be seen as parallel lines contained in a sphere, will at infinity arrive at the same point on the plane at infinity, because as we saw before, when the radius line of the sphere is infinite it is no longer a three-dimensional space.  The rounded sphere has become a plane, an all encompassing plane to be sure, surrounding from the infinite periphery (the unseen universe imagined by cosmologists) all that was at one time interior.  The surrounding geometric quality remains, but since space itself is transformed, it accomplishes a kind of paradoxical miracle.

To travel to infinity in one direction (in terms of the spherical three-dimensional nature of ordinary space) means to return from the opposite direction, for once within the plane at infinity, the line that intersected the ever flattening arc of the sphere is now simultaneously a point that is everywhere.  The point, in the center dimensionless, expands, first  becoming a growing measureless sphere until it ultimately becomes a plane.  Our geometric imagination never has to leave the proper and logical train of geometrical thought.  Once more: "Think on it: how the point becomes a sphere and yet remains itself.  Hast thou understood how the infinite sphere may be only a point, and then come again, for then the Infinite will shine forth for thee in the finite."  Rudolf Steiner.

If we then appreciate that the night sky is the plane at infinity, and that the measure we exported from our earthly perspective is not valid out there in cosmic space, then the light quanta, existing there outside of time and space, radiates toward us from this cosmic periphery, only becoming space-bound when within three-dimensional space.  At the periphery, light quanta are not limited by the so-called speed of light, but are everywhere at the same time, yet somehow differentiated, for that is what we see, not just with the eye but with all our instruments as well.   This violation of the previous limiting idea of the speed of light has now been disproved in certain quantum physics experiments (Google: Alain Aspect 1982).

Light comes towards us from the stellar reality.  If that reality is not spacial in the sense that we previously assumed (rooted in three-dimensionally matter based bodies like suns and planets), then what is it?   What can exist in the transitional space in between a true three-dimensional sphere, and the pure plane at infinity?  If out there is not an  empty space in which three dimensional matter arises, what does arise there in that space that, like the infinitesimally small, will not allow itself to conform to Earth-like physical laws?

These are the questions that have to be faced if we apply projective geometry to the relationship between our Earth center, and the peripheral plane at infinity.  If we look at the stellar phenomena, such as redshift, then what meaning can be attributed to that kind of existence which creates light that violates the rules we know at the Earth center?

Perhaps it would be better (disregarding the word "deeper" above) to think of these objects as more filled with Life.  The plane at infinity, as transformed space, reveals a high level of dynamic properties in all its light radiations.   Could that dynamism be Life? Why could we think that and remain within reason?

Something is happening out there that comes here.  Light is created out there and comes here.  Our science has made all kinds of pictures for us of what is happening out there, yet these pictures are not empirical, but entirely theoretical.  Moreover, they are entirely material and assume that the laws of physics at cosmic distances will be the same as they are on the Earth, which already we have noticed is not justified for the very very small.

If we work from the idea of the plane at infinity first (for which projective geometry grants us every right), then we might ask whether or not space itself is created out there.  We see the light coming toward us from the cosmos, and we notice its dynamic properties (all the various intensities of redshift, among others - Quasars, neutron stars etc).  If we discard measure (which projective geometry doesn't need), then the plane at infinity, with its inward radiating light is perhaps creating space itself, not from a point center (such as the Big Bang), but from the cosmic periphery.

The plane at infinity (transcendent of matter oriented three dimensionality) creates three dimensional space and time, by radiating light inwardly from the cosmic periphery.  Redshift is not old light receding, but its opposite - new light becoming space and time.  This is exactly the idea of a student of Rudolf Steiner's, George Adams Kaufmann, in his 1933 essay on cosmic theory (rooted in projective geometry): Space and the Light of Creation, which essay's first chapter is Radiation of Space (the second chapter is The Music of Number, and the third and last chapter is The Burden of Earth and the Sacrifice of Warmth). [This book small book on cosmic theory is quite difficult to find, although connecting to a Rudolf Steiner library may help.]

What kind of power could create Space itself?  Our point centered assumptions, working from only quantities, have only been able to think of a spiritless matter filled Universe, born in a Big Bang.  Certainly, working inwardly from the cosmic periphery (the plane at infinity) which the new geometry gives us every right to do, what is that which can be out there that rays inwardly the creation of Space itself?

"...and in it was life and the life was the light of the world..."  The power (fiat lux - let there be light) surrounding the Universe, is Life, and the Life creates the Light, and the Light rays inwardly creating Space and Time, in the center of which the Earth of living matter and substance arises, itself a narrow spherical band, for Earth life is only on the surface - go too deep and it is fire and there is no life, go too high and it is airless and again no life.

From the plane at infinity, through the inward plane-ward sculpted spheres of light, resting for a moment at the Earth periphery, where humanity unfolds its evolution, then eventually still collapsing to smaller and smaller spheres, ultimately disappearing into pure point centered geometric intersections of fields of force and the mysterious light quanta we discover in our laboratory experiments in quantum physics.   But is it light quanta that is born first in the cosmic periphery, and then flies inward ultimately dying into very very tiny points from out which are built living matter and substance?

Should not, according to the laws of symmetry so essential to projective geometry, there be both a similarity and a difference between the infinitely large and the infinitesimally small?  If life is created at the cosmic periphery, does it die into the very very small, only to be reborn instantaneously once more in the cosmic periphery?   Recall our imaginative experiment with the parallel lines.  If time and space rules don't apply to light quanta (photons), this will be true both at their point of first appearance and then again at their point of disappearance.

Yet, something not quite right here.  The measureless sphere exists in between the infinitely large and the infinitesimally small.  Appearance and disappearance are the same process in a way.  Here again is Rudolf Steiner: "Think on it: how the point becomes a sphere and yet remains itself.  Hast thou understood how the infinite sphere may be only a point, and then come again, for then the Infinite will shine forth for thee in the finite."

Created out of the uncreated and formless, generating space and time, falling then inward toward the center from the periphery until collapsing into the nothingness once more of timeless and space-less point centers, before returning instantaneously again to the cosmic infinite plane of life.

And, the simultaneously opposite:  Arising out of the uncreated and formless nature of the mysterious light quanta, radiating outward from an infinite number of point centers, spreading out toward the cosmic periphery, there to disappear into the remarkable spaceless and timeless plane at infinity.

A mystery aptly caught in the image of a mobile imagination of the gesture in space that creates the form we know as the lemniscate - the symbol for infinity.

Moreover, of all the mysterious facts quantum mechanics has discovered, it seems that it is the mind itself that determines the nature of the collapse from potential becoming (probability) into manifestation.  Consciousness is crucial.   Without consciousness there is no manifestation, only probability.   Could not a Larger more Infinite Consciousness exist at the Periphery, where time and space themselves are first manifested?  Then too, if the Great Mind can do that, what then is involved in the small mind, when it thinks and acts so as to unfold its own creative imagination and exact picture formation in learning of and practicing the measureless beauty of projective geometry?

In the Beginning was the Word, and the Word was toward God, and God was what the Word was.  It was with God in the Beginning.  All things happened through it, and not one thing that happened happened without out it.  In it was life, and the life was the light of the world....*

So Christ advises us to pray: "Our Father in the skies..."

*translation from the Greek of a part of the prologue to the John Gospel, from the book, The Unvarnished Gospels by Andy Gaus.

Of course, currently Natural Science hasn't the capacity to appreciate such a change in their understanding of the Cosmos.  But this book isn't written for scientists, its written for those Christians, who might like to have a sense that one can still be deeply religious and not abandon the rational.

What we have done, by the way, is look at the image building processes of the fine minds at work in natural science, which have created a kind of myth regarding the stellar world - a myth quite different from that held by more ancient minds in ages long ago.  We have not returned to those ancient myths so much, as taken up, out of the advancing progress of natural science itself, a particular discipline (projective or synthetic geometry - all geometry), and applied it to move past the current astronomical myth to what perhaps might well be the kind of truth the physicist pursues when he chases his holy grail of the so-called: Theory of Everything.  (See my latest book: The Art of God: an actual theory of Everything)

Most versions of the Theory of Everything rely on highly abstract mathematical complexities - a kind of near-secret symbolic language only useful to the priests of Natural Science.  Would it be possible to construct a Theory of Everything using ordinary language?  Can the symbols of words on a page and simple concepts, understandable by ordinary consciousness, produce a better Theory of Everything?  May it not be necessary in fact to reintroduce qualities and mix those with quantities, if we are actually going to have a true Theory of Everything?  Doesn't such a Theory not only have to explain consciousness, but our form of consciousness - why we live in the world in between the very very large and the very very small?

We have constructed this essay in a way that makes it possible for the naive consciousness to behold in their own minds something that so far has been presented to the world as a secret mystery only knowable to the mathematical adepts of the religion of natural science.

We live in a time when there are to be no more priests, of the religious or the scientific kind.  No more claims that the ordinary and naive mind has to be dependent on another for their understanding of the world and of the universe.

The Universe wants to be known, just as we want to be known.  "You see, for now we look as if in a mirror, shrouded in mystery; but then we will see face to face.  Now I partly discern; but then I will perceive the same way that I was perceived all along.  And so we will have faith, hope and love, these three: but the greatest of these is love."*

*[Andy Gaus, Unvarnished New Testament - end of chapter 13, of St. Paul's First Letter to the Corinthians.]

addendum

- many questions remain -

No reader should consider that the above has exhausted all the remarkable possibilities of projective geometry in advancing our understanding of the Nature World as it appears to both our senses and our scientific instruments.   All I have really done is try bring to light aspects of thinking and the imagination that many don't yet appreciate.

Nor is the above perfect by any means, for it is clearly the work of an amateur.  That fact, however, should not stop us from going onward and asking all the many questions that still need to be asked.  [As an aside: in my considerations of the nature of electricity and its relationship to Nature, I discuss how space itself needs to be carefully rethought in order to appreciate that "space" itself needs to be reconceived even as regards electrical and magnetic phenomena: "Electricity and the Spirit in Nature - a tale of certain considerations of the present state of science,  in the light of a modern practical understanding of the nature of mind".]

For example, does the plane at infinity collapse into one point, or into all points?  We can think of the very smallest, as we observe them in the local conditions of the earth in our laboratory experiments, as a very huge number of such point centers.  All matter and substance seems to be built up out of light quanta, and other oddly named particles.
 

Now a plane, which has no measure, is infinite in all directions.   It can also be constructed, under the well known rules of projective geometry, of points.   There is, in this geometry, a plane of points, a plane of lines, a point of lines, a point of planes, and a line of points and a line of planes.  If we recognize that the Plane at Infinity is made up of all possible points, then what keeps it from radiating toward our Earth-Center that which becomes all the many point centers from which matter and substance arise.  Once there, in this infinite number of point centers, that which has first radiated inward, returns once more to the periphery.  This our geometric imagination can experience.

A deep study of projective geometry reveals several kinds of processes which arise according to the basic relationships of plane, line and point; or, the source or origin of light (the plane at infinity), light becoming space and time (radiation of space) and light dying into the source once more through its collapse into the infinite number of point centers quantum physics discovers.  To this we add the process of that which radiates out from point centers towards the periphery.  In the light of understanding this, we can come to quite new conceptions of how crystals grow, and what is happening at the growing point of a plant.  Such work has been done, in fact, by the Goethean Scientists pointed out in the above essays.

In addition to these questions then we are right to ask another: what is the nature of the space occupied by the imagination itself?  We know this exists, and not only that it exists, but that we create it.  We consciously create imaginative space ourselves.  What are we that we can do something that has such kinship with the space and time creating activity of the Mystery at the Plane at Infinity?

"Imagination is more important than knowledge.  For knowledge is limited to all we now know and understand, while imagination embraces the entire world, and all there ever will be to know and understand." Albert Einstein [emphasis added, ed.]

- healing materialism -

The human being possesses a remarkable power in that he (or she) is able to make images and share them with others.  Meaning streams from one to another upon this product of the picture-thinking imagination.  We are taught science out of this image creation capacity.  We tell the wonderful stories of our ancestors out of this same image creation capacity.  What we frequently don't do well, is find a way to be scientific about this image creating capacity itself. 

Of all the scientific disciplines that will enhance this image building capacity, in a logically rigorous fashion, it is the discipline of projective geometry (as taught by such as Whicher above) that will be the most fruitful.   At the same time, the human being is more than rationality - much more.

That human culture produces art and religion, as well as science, ought to give us a significant clue.   Whicher's book takes account of this, to a degree, by including a number of pictures of art, including religious art.  What is less appreciated is the role of human intention, of human will, in all this (the will is the point-of-meaning center of the same consciousness which the quantum physicist recognizes is needed for the potential to collapse into the real).

At the end of the main body of the essay above, I tried to remind the reader that we are part of reality.  Quantum mechanics has seen this, for the potential of quantum events only collapses into actual space and time when our consciousness participates.  The genius of Owen Barfield discusses participation in detail, in his book Saving the Appearances: a study in idolatry.

In this book, through a wonderful examination of what the deeper study of human languages can reveal, Barfield shows us how there is an evolution of consciousness, to go along side the physical evolution so far discovered.  For Barfield, the quite ancient times could be called: original participation.  This was a time when the human consciousness was instinctively one with reality, thus giving birth to all the ancient myths.

This original participation eventually faded away, giving us an intermediate state, called by Barfield (and others): the on-looker separation.   Humanity is pushed out of the condition of original participation by the Gods themselves, so that we can by this independence learn to experience our freedom and our ego (self) consciousness.   The on-looker separation is itself marked by special changes in language, in art and also gives rise to natural science.   It is as on-lookers (forgetting our role as thinking observers) that we build the images of the natural world, both earthly and cosmic, as only matter and never spirit.

But the natural world will not submit for long to that false view, and so quantum mechanics finds that it must reinsert human consciousness into its concepts of the basic physics of the world.  With this now well established basic scientific knowledge, to which we can add the discipline of projective geometry (especially with its understanding of visual cones of light), the path is laid out of science itself toward what Barfield called then: final participation.

Quantum mechanics tells us that our consciousness is needed for the potential to be able to collapse into the real.  Projective Geometry tells us not just rules about the light cone of physical space, but as well the light cone of internal imaginative space.  Rudolf Steiner's introspective science (outlined in A Theory of Knowledge Implicit in Goethe's World Conception and The Philosophy of Freedom) shows us how to experience the world of image building (organic form) and concept creation (pure thinking) in a fully mature participatory way.

At the same time, I don't participate solely as a rational being, but as a being to whom art and the sacred have meaning.  In a certain sense, given the often raw nature of emotions, the human being is often simultaneously: irrational (overly emotional), rational (mentally disciplined) and transrational (capable of huge leaps of non-logical intuitional insight). If I add these dimensions of my being to my imaging building and conceptual formulations, what kind of picture of the world will I paint?  Given this question, I will end with a couple of stories as a kind of demonstration.

In the mid-seventies I was traveling with some friends in Northern California.  We were a group of adults and children, and during the day a few of the adults were designated camp-parents, while the others were free to wander farther.   Thus I found myself, on the evening of the Summer Solstice, sitting on a beach in Northern California watching the Sun set over the Pacific Ocean.

As the Sun set, the sky slowly grew darker and stars slowly appeared.   This is what I observed as I continued to watch the point on the horizon where the Sun had set.   Together, as a group, at the precisely same degree of arc of the edge of the ocean, there appeared three stars in a somewhat vertical line.   The Sun goes down, and soon thereafter where it went down a vertical line of three stars appears.

Now the reader should realize that I was at that time quite convinced of the spiritual reality of things, out of my own direct experience.   As a consequence, when I observed our natural world I perceived it as a teaching.  For example, we can observe that of all the many inorganic and organic beings that appear in visual space, there are a variety of forms.   Of this variety of forms, only one form, one shape, has hands that have been so creatively freed by our ability to be able to stand upright.

Moreover, this human being changes his living environment in profound ways.  We act upon the creation, as if it was within us that the creative power itself was slowly incarnating.  To my thinking then, there existed a kind of dialog between the world of the senses and my own inner being (the teaching).   Here I was on a beach watching the Sun, itself a very special form (we receive light and heat from it that are necessary for life - without the Sun we do not live).  As this form set on the Summer Solstice, the first stars to appear (the night teachers), were three.

This then is what the teaching sang to me on that beach: one becomes three.  So the Mystery of the Trinity was written right there in the most simple events of the world of the senses.  One becomes Three.

The ambient light became slightly dimmer, and not too soon thereafter, above the three was four, in the shape of a kind of box, standing on one of its corners above the last star of the three.  The One becomes Three and then Four is added to become Seven.  Those who know what is sometimes called the occult significance of Numbers will recognize here all manner of analogies, about which nothing more need be said. (for the more traditionally fixed of mind, the Sun set and in the order described, the constellation of the Great Bear emerged, standing on its tail above the same place on the horizon the Sun had set on the night of that particular  Summer Solstice - yet this constellation did not appear all at once, but in a very definite sequence as the day light faded and the night lights manifested themselves).

In this way I was initiated more deeply into the Mystery of the Night Teachers, and while I wished my life would have allowed me to study over many decades this teaching by which we noted not just the starry sky, but when and in what order the stars emerged, I did then realize that those who observed from such as Stonehenge saw a world of wonder we have still yet to fully appreciate.

One more similar picture.  If the shape of the sense world is from a Creator, and this Creator is such profound Mystery that we have hardly yet begun to appreciate all the He has done and is doing, should we be surprised by the manner and depth of the teaching that awaits us both within and without?   Consider, sunrise and sunset.   Something that happens all over the world everyday, and has done so for eons.

If we, as an aspect of final participation, re-ensoul the world of the senses with being and consciousness, might we not then begin to see that when the Sun sets, when the shape representing (in its speaking-teaching) the Highest of the Mystery, recedes from our sight, at that moment the stars, one by one and then in groups, slowly emerge, slowly appear in the dark and by their order of appearing and by the shapes and forms they thereby render, they can be seen as singing praises to this Highest.   He sets, and they rise and sing.

Then the night ends, the regular night-singing has passed, and as the Sun begins to once more return to shed Its light and warmth and life on humankind, the stars recede, and kneeling down, in groups and then one by one, they give way to that which they honor above all else.  Yet, this is not all.

For the shape of time and space, of stars and suns and the world of humankind, is also teaching.  We are there too, and what are we, we human beings, that the Highest and all the Angels look down upon us - surround us and gift us with such Love we hardly appreciate it.  Not just that but more, for we are not only looked down upon from Above, but we are also carried through cosmic space by the Earth - Father Sky and Mother Earth - as the world's oldest peoples and cultures well know.

The dark moist earth is the Mother, from which all that grows and nourishes flows.  The waters that give life, the very air we need to breath.   There in the center of all, looked down upon by Father Sky, upheld and nourished in the Womb of Mother Earth, sits the human being, the upright shape with the hands and the creative and curious mind.  That is the real question of final participation: Who are we?